Introduction to Depth-First Search (DFS)
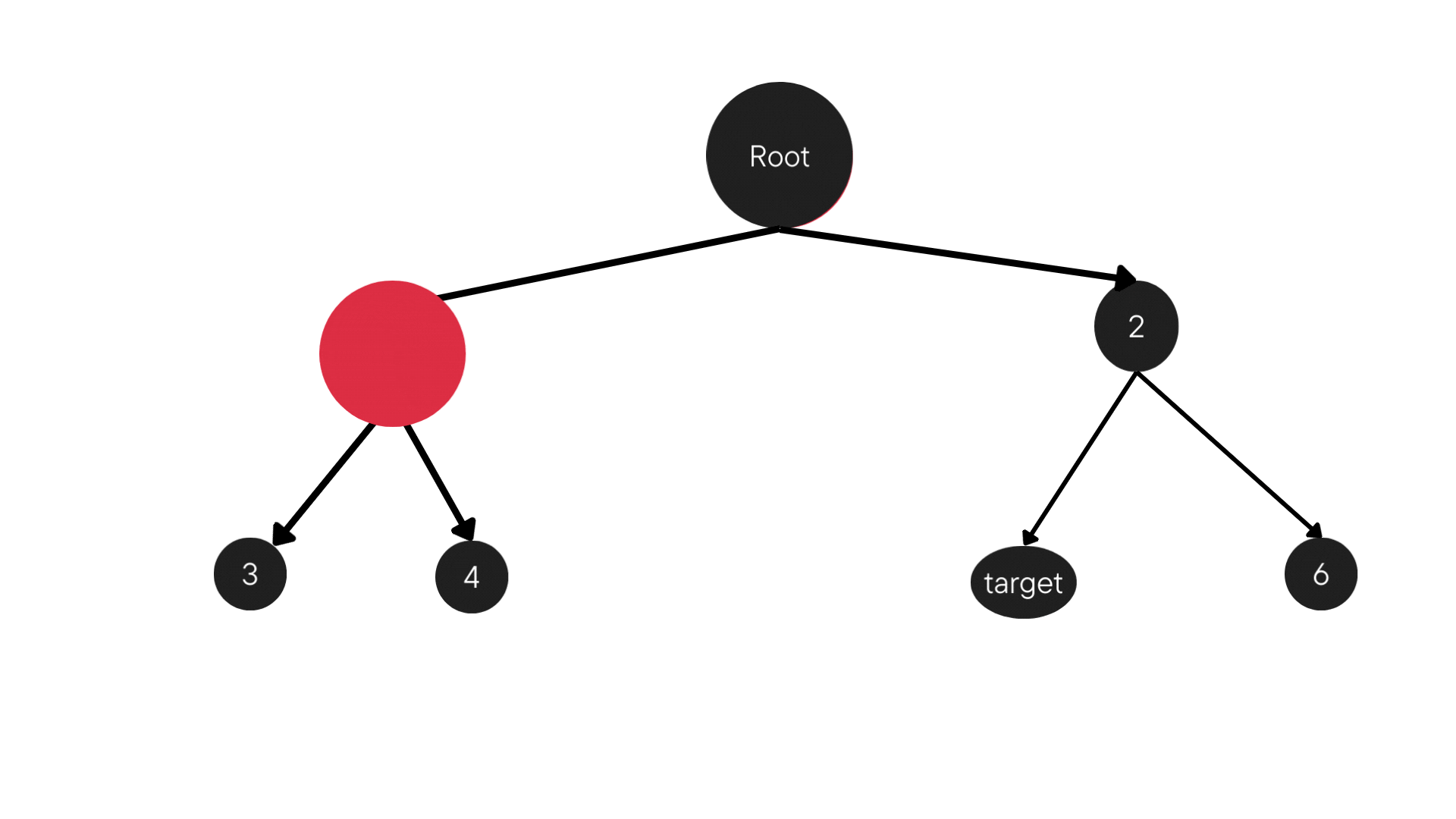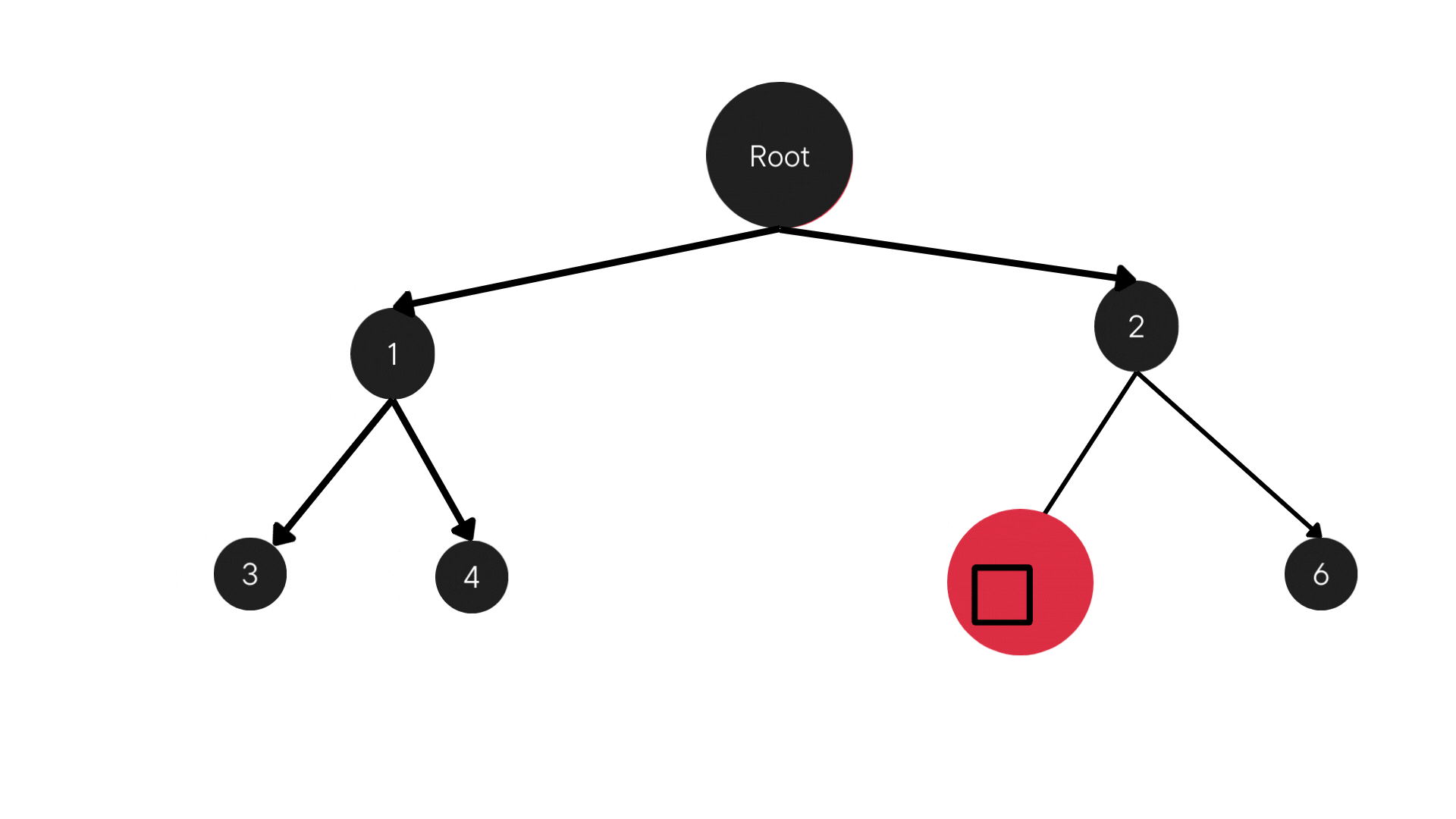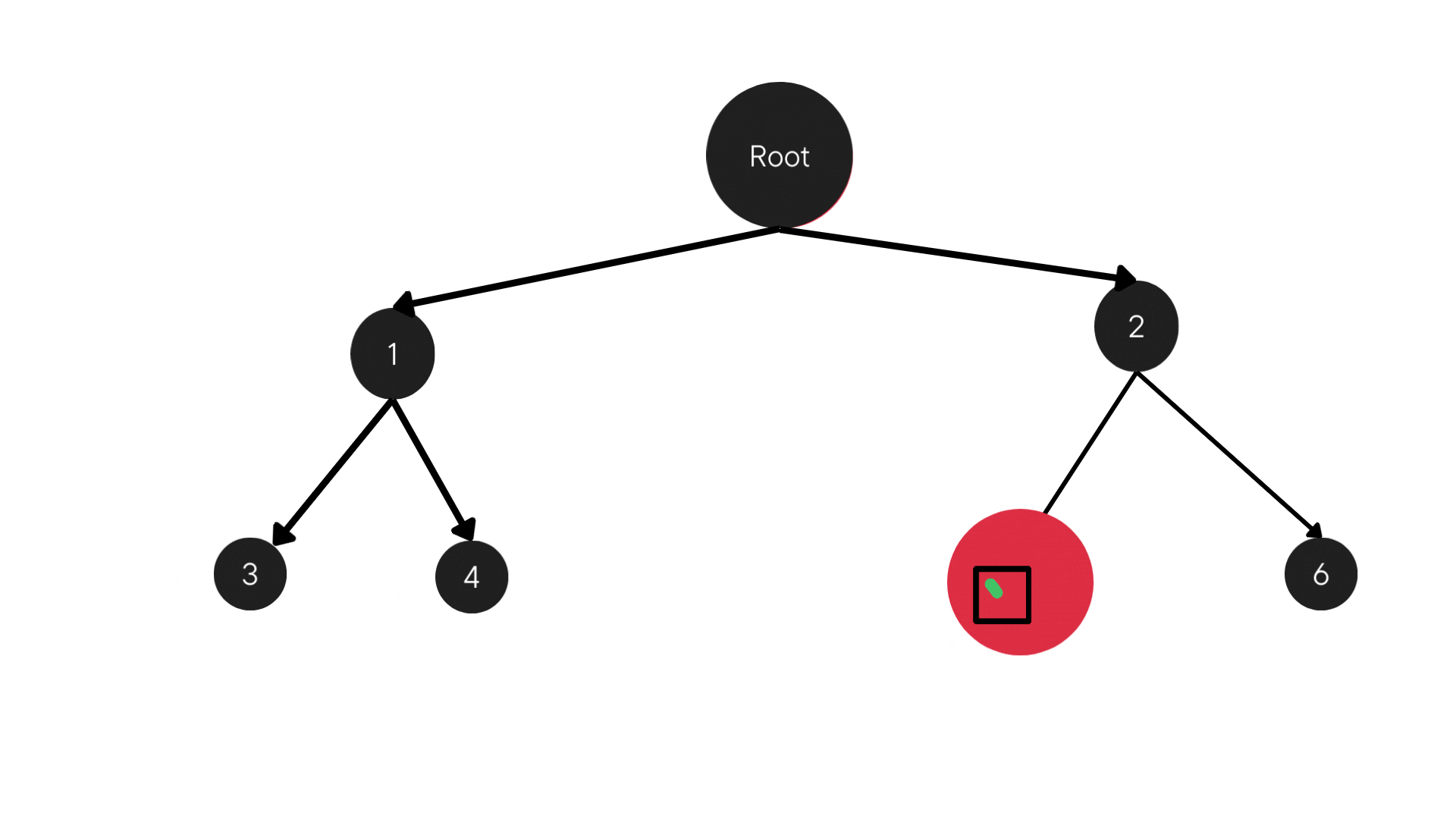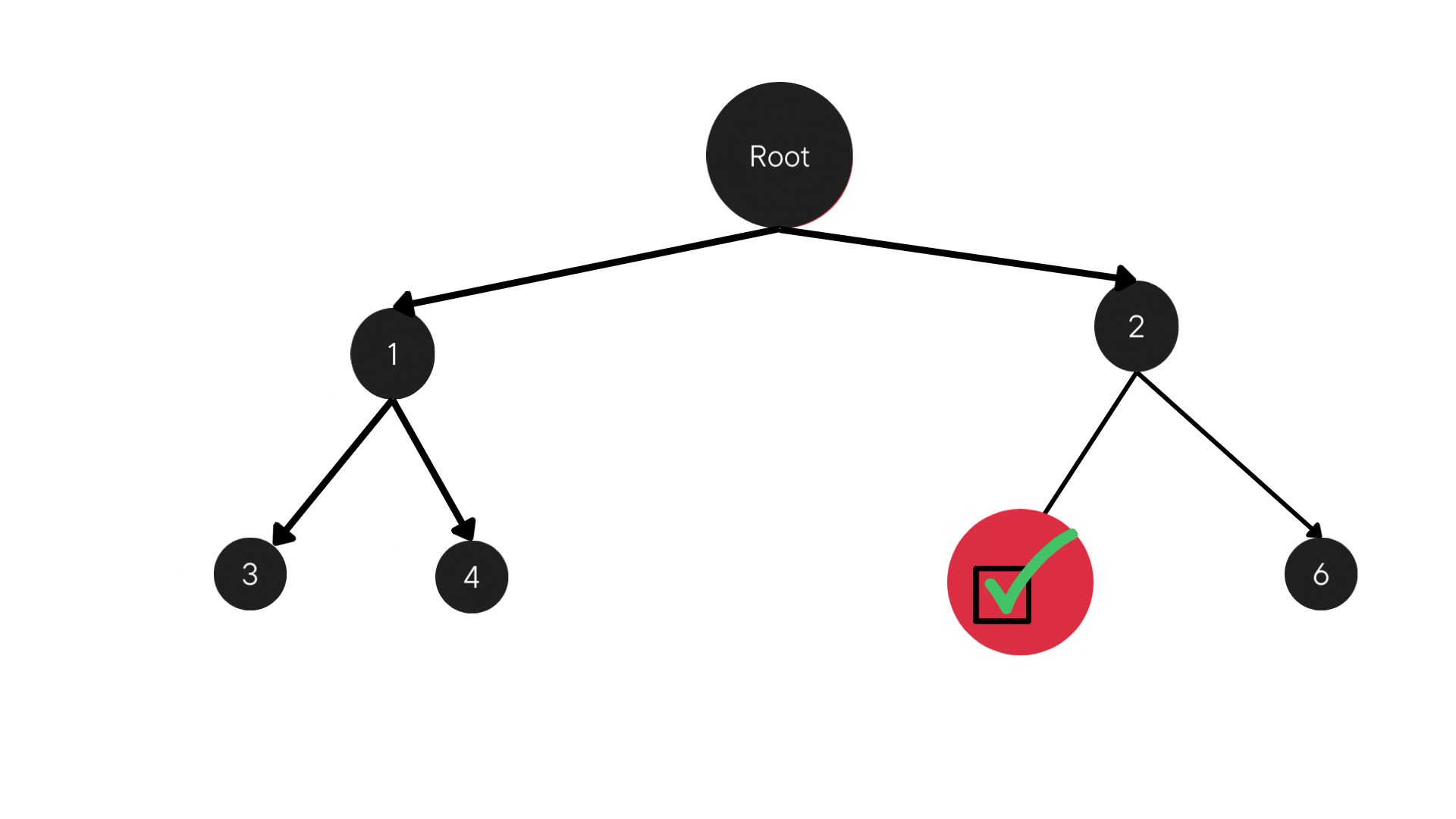
DFS is a graph traversal algorithm. It is designed to explore a graph's nodes. DFS is unlike its counterpart, Breadth-First Search (BFS). It goes deep into the graph before backtracking. The algorithm is recursive or stack-based. It visits a node and explores each branch as far as possible before backtracking.
Understanding the Core of DFS
Graph Traversal Mechanics
Depth-First Search (DFS) is a graph traversal algorithm designed to systematically explore a graph's nodes. Unlike its counterpart, Breadth-First Search (BFS), DFS plunges deep into the graph structure before backtracking. The algorithm follows a recursive or stack-based approach, visiting a node and recursively exploring as far as possible along each branch before backtracking.
The Graph Representation
Consider a graph with a designated root node and its children, each node having a specific branching factor – the maximum number of children a node can have. The DFS algorithm starts at the root, explores as deeply as possible along each branch, and backtracks only when necessary.
def find_target(self, curr_node, target_node, path, depth):
"""
Recursively searches for the target node in the graph.
:param curr_node: The current node being explored.
:param target_node: The target node to search for.
:param path: The path taken during the search.
:param depth: The current depth of the search.
:return: A tuple containing a boolean indicating if the target is found and the path taken.
"""
# Check if the current node is the target node
if curr_node.uuid == target_node:
return True, path
# Check if the depth has reached the specified limit
elif depth >= self.depth:
return False, []
# Initialize a tuple to track if target is found and the path
target_found = (False, [])
# Append the current node's uuid to the path
path.append(curr_node.uuid)
# Iterate over the children of the current node
for child in curr_node.children:
# Recursively call find_target for each child
target_found = target_found[0] or self.find_target(child, target_node, path, depth + 1)
# If the target is found, return the result immediately
if target_found[0]:
return target_found
# Remove the current node's uuid from the path if target not found in its children
path.pop()
# Return the final result
return False, path
Time Complexity Analysis
The time complexity of DFS depends on the depth of the graph and the target node's location. In the worst case, the target node is at the deepest depth. Then, the time complexity becomes exponential. A detailed analysis involves counting the nodes at each depth. This requires considering the branching factor.
To calculate the time complexity of DFS, we would need to consider the worst case. What's the worst case? The worst case is when our target value is at the right most branch of the graph. In that case we would need to discover all the nodes before reaching the rightmost value. In that case, we would need to traverse all the nodes in the graph. So now, the question becomes, how many total nodes are in the graph.
Considering a branching factor = b, the total number of nodes will be:
Total nondes = b^0 + b^1 + b^2 + b^3 ≅ b^n
i.e. T(n) ≅ b^n
Space Complexity Considerations
The space complexity in DFS mainly depends on the graph's depth. The algorithm uses a stack or recursive call stack to traverse the graph. The depth reached during traversal sets the space complexity. It's denoted as O(h), with h as the max depth.
O(h) = h // We just store h elements in our recursive stack
Python Implementation
Crafting a Python DFS Class
Let's transition to the practical side of our exploration – a Python implementation of DFS. The code comprises a Node class representing graph nodes and a DFS class with methods for graph construction and target node search. The DFS algorithm is implemented using recursion and backtracking.
from collections import deque
class Node:
# Class variable to keep track of node numbers
nodeNumber = 0
def __init__(self):
# Increment the nodeNumber for each new node
Node.nodeNumber = Node.nodeNumber + 1
# Unique identifier for the node
self.uuid = Node.nodeNumber
print("Building: ", self.uuid)
# List to store children nodes
self.children = []
def construct_and_get_child_node(self, child: object) -> object:
"""
Constructs a child node and appends it to the current node's children list.
:param child: The child node to be appended.
:return: The appended child node.
"""
self.children.append(child)
return child
def __eq__(self, other):
# Custom equality check based on uuid
return self.uuid == other.uuid
class DFS:
def __init__(self):
# Initialize DFS with root, current node, branching factor, and depth
self.root = None
self.curr = None
self.branching_factor = None
self.depth = None
@staticmethod
def build_child_nodes_breadth_first(root, branching_factor, depth):
"""
Builds child nodes in a breadth-first manner up to a specified depth.
:param root: The root node.
:param branching_factor: The maximum number of children for each node.
:param depth: The depth of the graph.
:return: None
"""
if depth <= 0:
return
queue = deque([(root, 0)])
while queue:
current_node, current_depth = queue.popleft()
if current_depth >= depth:
return
for idx in range(1, branching_factor + 1):
child_node = current_node.construct_and_get_child_node(Node())
queue.append((child_node, current_depth + 1))
def search(self, target_node):
"""
Initiates the search for a target node in the graph.
:param target_node: The target node to search for.
:return: A tuple containing a boolean indicating if the target is found and the path taken.
"""
self.curr = self.root
path = []
return self.find_target(self.curr, target_node, path, 0)
def find_target(self, curr_node, target_node, path, depth):
"""
Recursively searches for the target node in the graph.
:param curr_node: The current node being explored.
:param target_node: The target node to search for.
:param path: The path taken during the search.
:param depth: The current depth of the search.
:return: A tuple containing a boolean indicating if the target is found and the path taken.
"""
# Check if the current node is the target node
if curr_node.uuid == target_node:
return True, path
# Check if the depth has reached the specified limit
elif depth >= self.depth:
return False, []
# Initialize a tuple to track if target is found and the path
target_found = (False, [])
# Append the current node's uuid to the path
path.append(curr_node.uuid)
# Iterate over the children of the current node
for child in curr_node.children:
# Recursively call find_target for each child
target_found = target_found[0] or self.find_target(child, target_node, path, depth + 1)
# If the target is found, return the result immediately
if target_found[0]:
return target_found
# Remove the current node's uuid from the path if target not found in its children
path.pop()
# Return the final result
return False, path
def pretty_print_graph(self, node, indent=0, parent_arrow=""):
"""
Pretty prints the graph structure.
:param node: The current node being printed.
:param indent: The indentation level for formatting.
:param parent_arrow: The arrow indicating the relationship with the parent node.
:return: None
"""
print(" " * indent + f"{parent_arrow}Node: {node.uuid}")
for child in node.children:
self.pretty_print_graph(child, indent + 1, "│")
def print_graph(self):
# Initiates the pretty printing of the graph from the root node
self.pretty_print_graph(self.root)
def build_graph(self, branching_factor=3, depth=3):
"""
Builds the graph structure with specified branching factor and depth.
:param branching_factor: The maximum number of children for each node.
:param depth: The depth of the graph.
:return: None
"""
self.root = Node()
self.branching_factor = branching_factor
self.depth = depth
return DFS.build_child_nodes_breadth_first(self.root, branching_factor, depth)
# Instantiate DFS
dfs = DFS()
# Build the graph with default parameters
dfs.build_graph()
print("Total nodes: ", Node.nodeNumber)
# Search for a target node (39)
path = dfs.search(39)
print(path)
TL;DR
This guide has equipped you with a detailed understanding of DFS, from its traversal mechanics to time and space complexities. The provided Python implementation serves as a practical demonstration of the algorithm's application.
Feel free to explore the code, experiment with different graphs, and deepen your grasp of DFS. As you navigate the technical depths, may your algorithms run efficiently and your coding endeavors be met with success.
Happy coding, and may your technical explorations lead to new insights and achievements!
If you have any questions or need clarification, feel free to email me at gautamsharma2813@gmail.com.
Signing off,
-G
